매일 매일 2200rating이하들 문제 못푼것중에 하나 골라서 풀고 있다.
2200짜리 문제였는데, 내가 풀이를 보지 않고 푼 것중에 가장 rating이 높은것 같다.
게다가, 정말 educational한 문제인거 같아서 마음에 들어 풀이를 쓰려고 한다.
https://codeforces.com/contest/1537/problem/F
Problem - F - Codeforces
codeforces.com
문제 한줄요약
간선을 골라 양끝점의 가중치에 임의의 정수를 더할 수 있다.
모든 정점들의 가중치를 주어진 배열대로 만들 수 있는가?
사실 내가 최근에 푼 여러 그래프 문제풀이중에 중간에 부분 문제를 coloring으로 환원 시키는 여러가지 문제가 있었다.
(이것도 애드혹 중에 하나 인가? 좀 유명한 테크닉 정도로 치부할 수 있을거 같은데)
https://codeforces.com/problemset/problem/1547/G
https://codeforces.com/contest/1385/problem/E
(이번 scpc의 c번도 문제자체가 유사해서 쓸수 있다.)
더 많은 문제가 있는 것 같지만, 최근 일주일안에 저렇게 3문제 정도나 풀고 간 상태에서 이 문제를 만났는데,
coloring으로 치환하는 법이 생각이 나서 해결해버렸다. 본 콘테스트에서는 E1에서 뇌절을 박아 E1까지밖에 못풀었는데, (E2는 정해가 z를 쓰거나 해싱박는 문제라 별로 이쁘단 생각은 안들고), F번을 봤었다면 더 좋았을것 같기도 하다.
풀이를 해보면, 가장 중요한 첫번째 관찰은, 간선 2개를 선택하는 것이 아니라, 정점 2개를 선택하자라는 것이다.

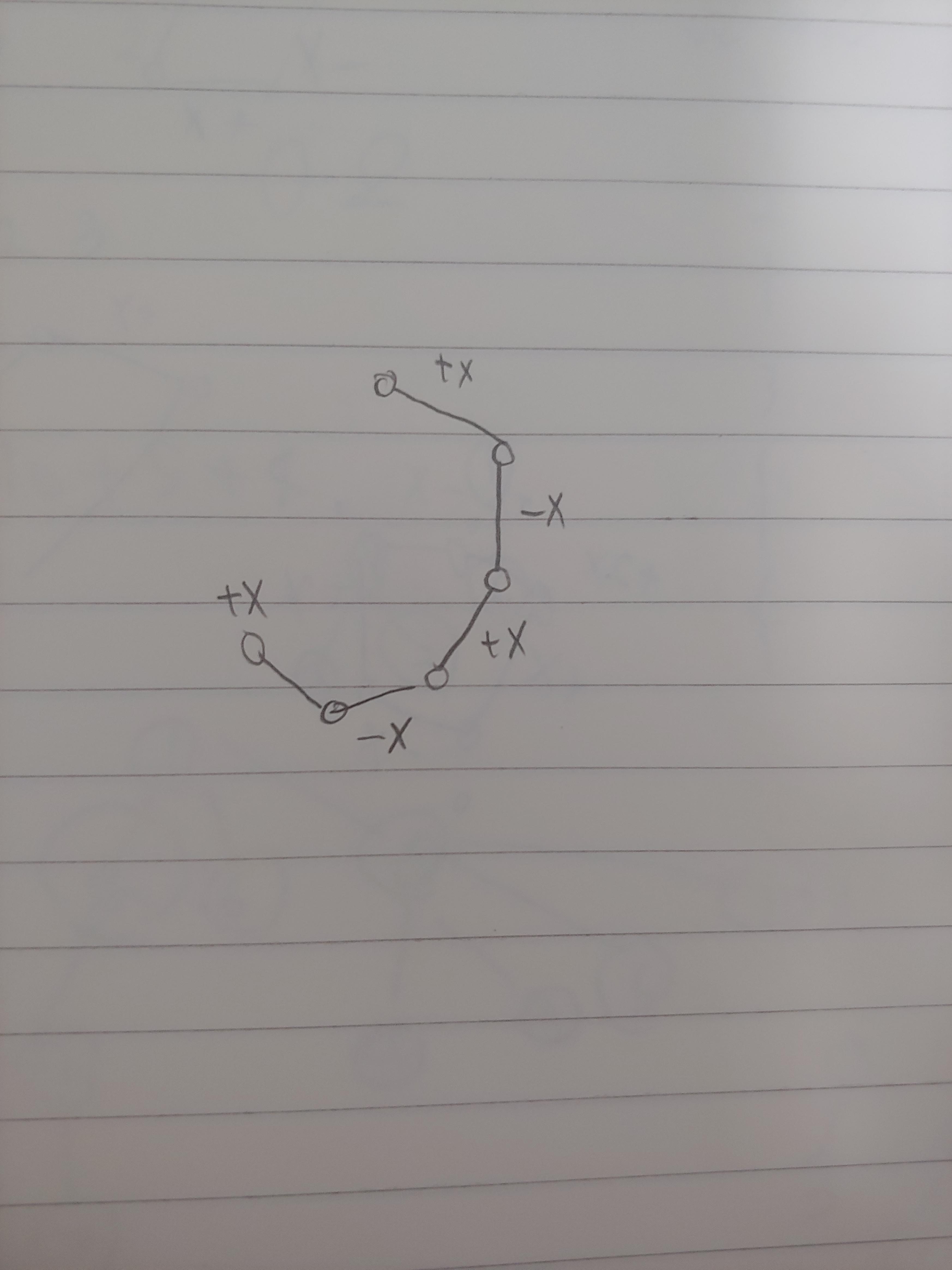
시작점과 끝점 빼고 모든 정점에는 가중치 변화가 없다.
그리고 시작점과 끝점 사이의 거리가 짝수일때는, 시작점은 +x, 끝점은 -x
홀수일때는 시작점 +x,끝점도 +x만큼 정확히 가중치가 변화한다.
우리는 무한번 사용할수 있으므로 x대신 1을써도 무방하다.
즉 이런 관찰을 하고 나면, 항상 인접한 정점에, 임의의 가중치를 더하고 빼는 대신에,
정점 2개를 잡고 가중치를 더하고 뺄수 있다! 홀짝 여부에 따라서 부호만 반대인채로
그런데 그래프에 사이클이 있을 수 있기에, 어떤 두 정점 사이의 거리는 홀수이거나,짝수이거나,홀수도 될수 있고,짝수도 될수있는 3가지 경우가 나온다.
이걸 이용해 coloring을 하는 거다.
한 정점(나는 1로 잡았다.)을 기준으로 dfs를 돌리는데 dp로 coloring을 해간다. 즉 홀수는 0번 색, 짝수는 1번색,둘다 되는건 2번색으로 색칠을 해가는데, 이미 색칠되어 있는 색을 다시 전파시킬 필요가 없다는걸 생각을 해보면 $N*3$번의 연산안에 모든 색칠이 완료된다.
그럼 문제가 끝날까?
아니다. 이제 문제 해결을 위한 단 한가지 걸음만이 남아있다.
2로색칠된 모든 정점들의 변화량을 free라는 변수에 더하자.
우리는 이제 남은 것들을 적절히 나누어서, 목표를 만족시켜야 하는데 즉 변화량은 줄고,free로 크게 만드는게 이득이다.
사실 여기서 1틀했는데 1번 정점에 모든 걸 꼴아박으면 될거라 생각했는데 아니다.
즉 무슨 말이나면, 예를들어서 가중치가 더 커져야 하는 정점이던, 작아져야 하는 정점이던, 홀짝이 정해지면 정해져버린다. (고정을 시키면)
그래서 https://codeforces.com/contest/1546/problem/A
이 문제의 아이디어를 가져온다.
+랑 -를 상쇄를 시키고, free를 최대한 이용하자는 것이다.
(제가 이 부분은 설명을 잘 못했는데 코드를 봐주세요.. ㅠ)
마지막엔 2로나눈 나머지도 고려해준다. 끝.
#include <bits/stdc++.h>
#define all(v) v.begin(),v.end()
using namespace std;
using ll = long long;
using P = pair<ll, ll>;
using PP = pair<ll, P>;
const ll n_ = 2e5 + 100, inf = 1e18, mod = 1e9 + 7, sqrtN = 333, p = 27;
ll dy[4] = { -1,0,1,0 }, dx[4] = { 0,1,0,-1 };
ll n, m, k, tc = 1, a, b, c, d, sum, x, y, z, base, ans;
ll gcd(ll x, ll y) {
if (!y)return x;
return gcd(y, x % y);
}
vector<ll>v[n_], A, B;
ll dp[n_][3];//dp[i][0]->거리 짝수,dp[i][1]->거리 홀수, dp[i][2]->둘다 됨.
void dfs(ll x, ll y) {
for (ll nxt : v[x]) {
if (y == 2) {
if (dp[nxt][2])continue;
dp[nxt][2] = true;
dfs(nxt, 2);
continue;
}
if (dp[nxt][(y + 1) % 2])continue;
dp[nxt][(y + 1) % 2] = true;
if (dp[nxt][y] && !dp[nxt][2]) {
dp[nxt][2] = true;
dfs(nxt, 2);
continue;
}
dfs(nxt, (y + 1) % 2);
}
}
void solve() {
cin >> n >> m;
for (int i = 1; i <= n; i++)v[i].clear(), dp[i][0] = 0, dp[i][1] = 0, dp[i][2] = 0;
A.resize(n + 1), B.resize(n + 1);
for (int i = 1; i <= n; i++)cin >> A[i];
for (int i = 1; i <= n; i++)cin >> B[i];
ans = 0;
while (m--) {
cin >> a >> b;
v[a].push_back(b);
v[b].push_back(a);
}
dp[1][0] = 1;
dfs(1, 0);
ll free = 0, ans = 0;
for (int i = 1; i <= n; i++) {
if (dp[i][2])free += abs(B[i] - A[i]);
else if (dp[i][1])ans += B[i] - A[i];
else ans -= B[i] - A[i];
}
if (free % 2 == abs(ans) % 2 && free >= abs(ans))cout << "YES";
else cout << "NO";
cout << '\n';
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> tc;
while (tc--)solve();
}'알고리즘 공부 > codeforces' 카테고리의 다른 글
| Codeforces Global Round 17/ D. Not Quite Lee (0) | 2021.11.29 |
|---|---|
| 자랑 (5) | 2021.10.11 |
| #557 Virtual contest (0) | 2021.02.05 |
| 에듀-102 (0) | 2021.01.16 |
| Codeforces Round #683 (Div. 2, by Meet IT) (0) | 2020.11.16 |